A Remark on Density Theorems for Riemann’s Zeta-function: 2

Table of Links

• 1
• 2
• 3 Proof of Theorem 1
• References

2

The goal of the present work is

(i) to give a possibly simple proof for all values of σ > 3/4, i.e. η < 1/4, which

(ii) breaks the DH for the non-negligible range σ ≥ 7/8, i.e. η ≤ 1/8, further gives

(iii) explicit density theorems for different ranges of all η < 1/4 with B(η) → 0 as η → 0 and

(iv) besides the (possibly indispensable) simple idea of Hal´asz uses only classical knowledge of the theory of Riemann’s zeta-function (classical in the sense that known since at least hundred years).

This means that we avoid the use of Tur´an’s method, the large sieve, Vinogradov’s method, further mean and large value theorems. However, to break the DH we need the estimate reached by the Weyl–Hardy–Littlewood method [Lit1922] (see also (5.15.1) of the book of Titchmarsh [Tit1951], 2nd edition, or the paper of Landau [Lan1924]):

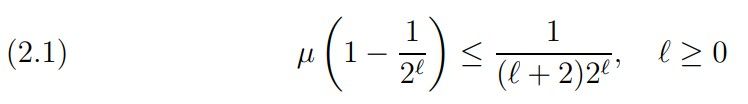
which is proved by Hardy and Littlewood in [Lit1922] for ℓ ≥ 1, but it is also true for ℓ = 0 (µ(0) = 1/2) by the functional equation and µ(1) = 0.

Alternatively, the method of Van der Corput would yield results of similar type [Cor1921], [Cor1922]. However, the use of (2.1) seems to be simpler, although Van der Corput’s result

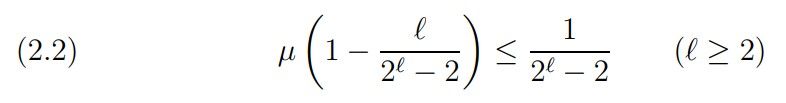
may yield even stronger estimates for N(1 − η, T) in many ranges of η. In order to formulate our results we need some more notation. For ℓ ≥ 1 let

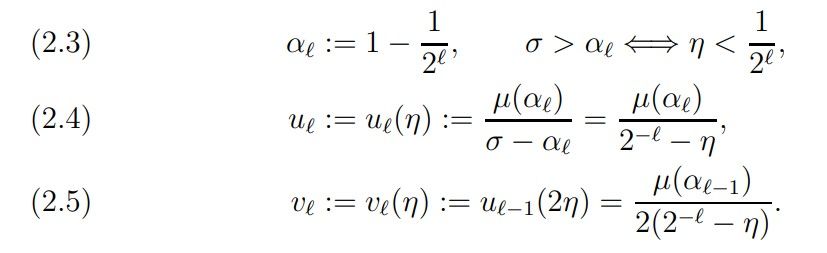
By the estimate (2.1) of Hardy and Littlewood we have for η < 1/2 ℓ

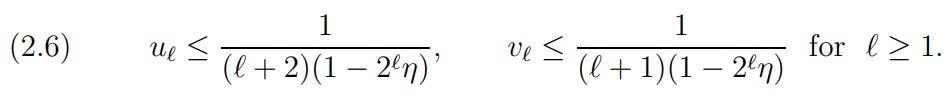
Theorem 1. For ℓ ≥ 1, η < max(1/3, 2 −ℓ) we have

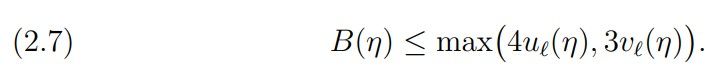
This implies a series of explicit density theorems for small values of η and the conditional result of Hal´asz and Tur´an [HT1969] that assuming (LH) we have N(σ, T) ≪ Tε for σ > 3/4, which is for σ > 3/4 a strong improvement of the theorem of Ingham [Ing1937] stating A(σ) = 2 for σ > 1/2 on LH.

Corollary 1. The Lindel¨of Hypothesis implies

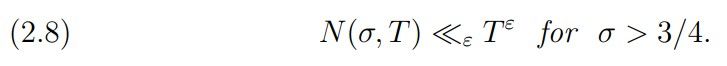
Proof. Choosing ℓ = 2, LH and the definition (2.4)–(2.5) yield uℓ(η) = vℓ(η) = 0 for η < 1/4.

Corollary 2. For ℓ ≥ 2, η < 1/2ℓ we have

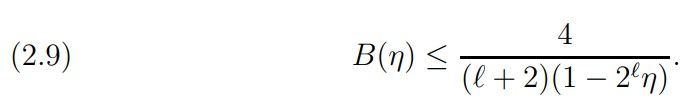
Proof. 4/(ℓ + 2) ≥ 3/(ℓ + 1) for ℓ ≥ 2 with equality for ℓ = 2. Denoting by log2 x the logarithm of base 2 and choosing C large (C = C(η) → ∞ as η → 0, but with C(η) = o(log 1/η)), we obtain for η ∈

[1/2 ℓ(1+o(1)) , 1/2 ℓ+C] from (2.7).

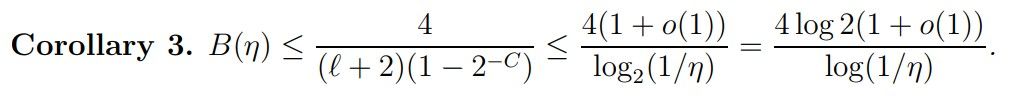
This is naturally weaker than a result obtainable by Vinogradov’s method (see [Pin2023] and [Hea2017]) but shows still B(η) → 0 as η → 0 beyond breaking DH in some interval for σ = 1 − η close to the point s = 1.

However, Corollary 2 yields also interesting (although already known) consequences form small values of ℓ (ℓ = 2, 3, for example), i.e., for relatively large ranges of η. On the other hand, they are often stronger than earlier results proved in a more complicated way (as 11.30 of Ivic [Ivi1985], for example).

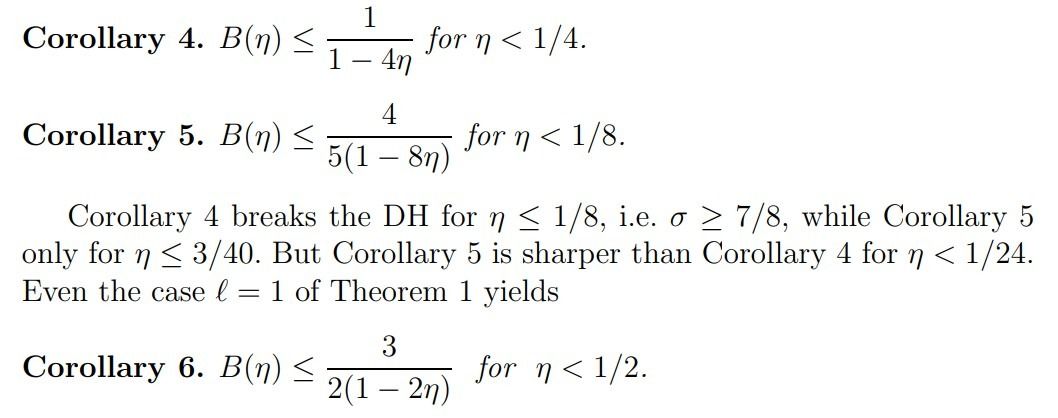
This breaks the DH also for η ≤ 1/8, that is, for σ ≥ 7/8, but it is weaker than Corollary 4 for η < 1/8 (sharper for η > 1/8).

Remark 1. Corollary 6 is trivial for η ≥ 2/7, i.e. σ ≤ 5/7.

Remark 2. It is an interesting feature of Corollary 6 that it gives a non-trivial result even in the range η ∈ [1/4, 2/7] in contrary to most applications of Hal´asz’s method, although it is weaker there than the classical theorem of Carlson [Car1920] or the one of Ingham [Ing1940].

Remark 3. It is also interesting to note that the case ℓ = 1 would yield the inequality of Corollary 6 with any estimate µ(1/2) ≤ 3/16 and any estimate of type µ(1/2) ≤ 1/4 − c2 (c2 > 0) would break the DH for η < c3(c2) with c3(c2) > 0.

Finally, similarly to Theorem 1 we can give an alternative proof of the case (12.10) of Theorem 12.1 of Montgomery [Mon1971] which states

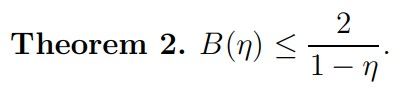
Remark 4. This represents a slight improvement of the Theorem of Tur´an (cf. (1.12)–(1.13)) since

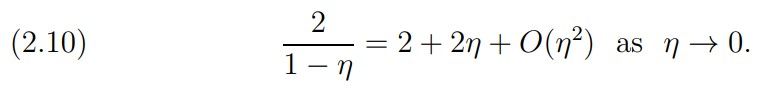
Remark 5. The proof of Theorem 2 does not need for any ℓ the estimate (2.1) of Hardy and Littlewood or the estimate of Van der Corput (apart from the “trivial” case µ(0) = 1/2 following from the functional equation).