Authors:
(1) Wahei Hara;
(2) Yuki Hirano.
Table of Links
- Abstract and Intro
- Exchanges and Mutations of modifying modules
- Quasi-symmetric representation and GIT quotient
- Main results
- Applications to Calabi-Yau complete intersections
- Appendix A. Matrix factorizations
- Appendix B. List of Notation
- References
Appendix A. Matrix factorizations
This appendix recalls definitions and fundamental properties of derived factorization categories. See [Pos, BFK1, BDFIK, Hir1, Hir3] for more details.





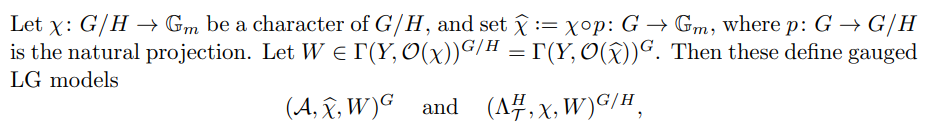
where W in the left LG model denotes f ∗W by abuse of notation, and the functor (A.A) defines the right derived functor
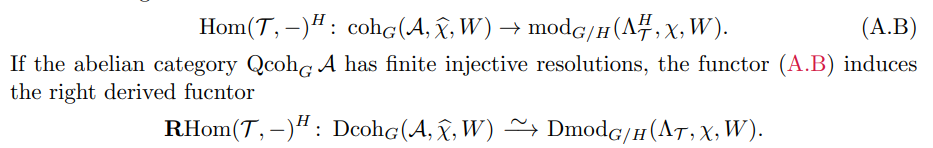
The following shows an equivariant and factorization version of a tilting equivalence.
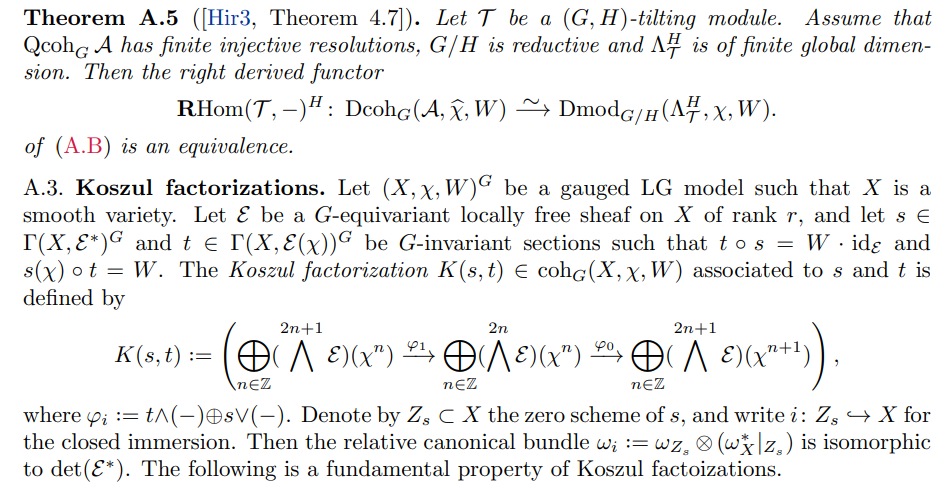
Lemma A.6 ([BFK1, Proposition 3.20][1]). Assume that the sections s and t ∗ are regular. Then there are isomorphisms
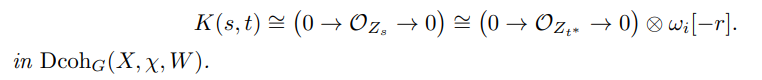
This paper is available on arxiv under CC0 1.0 DEED license.
[1] There is a typo in the latter assertion in loc. cit.
